Is it chance? Use a T-Test to identify how likely an intervention worked
| Topic Infobox | |
|---|---|
| Linked pages on this wiki | Tools (1), |
- This article is about when and how to do statistical testing with t-tests. For a broader article on statistics, see Statistical testing.
A frequent problem in personal science is that you tried an intervention and want to see if it worked. But you are unsure whether any differences you observed are maybe just by chance. So how can you see how likely is it that the results were chance? One of the simplest tests is a T-Test, sometimes called a “Student T Test”[1], which provides you with a p-value after doing the t-test.
Background[edit | edit source]
Generally, statisticians use the concept of p-values to discuss how often you would expect to observe the effect you did observe just by chance. A a simplified example, a p-value of 0.05 means that you would randomly observe this effect in 5 out of 100 retries of your intervention just by pure chance. While this crude measure doesn’t describe all the ways something might happen due to chance, generally the lower the p-value, the better.
Professional scientists, especially those who understand statistics, are skeptical of claiming a result based purely on p-values, but for Personal Science purposes, it’s a good start. There is no “correct” p-value cutoff that determines whether an effect is not due to chance alone, but traditionally people assume that any p-value that is smaller than 0.05 deserves a closer look and indicates that is probably a 'real' effect.
What you need[edit | edit source]
To be able to perform a t-test you need your numerical data which is split into exactly two conditions. Depending on the kind of intervention you did there are two different ways to split your data:
- Grouped (also called 'paired') data, e.g. measurements are taken before and after the intervention, always creating a pair of data. An example of this would be if you regularly measure your blood pressure immediately before drinking a coffee and then take a second measurement after the consumption. This way each time you do the intervention you generates a pair of data.
- Independently sampled data, e.g. when there is no clear before/after. As an example, suppose you would like to know if taking a Melatonin supplement will help you sleep longer. You measure your daily sleep, taking the supplements on some days (the “intervention”) and not on others (“control”). Each night of sleep data now either goes into the intervention or control group.
In order to perform a grouped/paired t-test you will need exactly the same amount of observations in both groups to keep the pairing. For independently sampled data this is not the case, i.e. you still do an independent t-test if you have more observations for interventions than controls (or vice versa).
Tails in a t-test[edit | edit source]
To perform a t-test one also needs to decide on whether one wants to perform a one-tailed or two-tailed test.
Broadly speaking, a two-tailed t-test is used to evaluate whether there is any difference between the two groups between the test was performed. When doing a two-tailed test, a small p-value indicates that there is a numerical difference between the groups but it does not indicate which of the two groups has the larger or smaller numerical values (but this can be verified through looking at the averages in each group).
For the one-tailed t-test one needs to specify the direction of the difference that one wants to test for. When doing a one-tailed test, the p-value indicates whether the values of one group are significantly larger (or smaller, dependent on the direction one chose) than for the other group but does not give any indication for the alternative.
As an example, a large p-value when using a one-tailed test to find out whether coffee lowers a persons blood pressure does not rule out that the blood pressure after drinking coffee has actually increased. It just means that we know it probably has not lowered. In contrast, if the same data would have been analysed with a two-tailed test and had resulted in a large p-value we would assume that the blood pressure has neither increased nor decreased.
One- or two-tailed test? Benefits & drawbacks[edit | edit source]
One- and two-tailed tests have their own benefits and drawbacks: Doing a one-tailed test is more sensitive – e.g. the p-values become low more quickly if there is real effect – than the two-tailed test. This increase in sensitivity comes at the cost of having to specify a clear direction and not being able to find differences which go against the selection of direction. Depending on your question, this might be acceptable or not.
For example, you might only worry whether coffee increases your blood pressure but would not be interested in if coffee might actually decrease your blood pressure. In other cases you might want to know if an intervention has any effect, be it positive or negative. In these and cases where you do not have a clear prior expectation using a two-tailed test might be worth even at the cost of some sensitivity.
Practical examples[edit | edit source]
t-tests in Excel[edit | edit source]
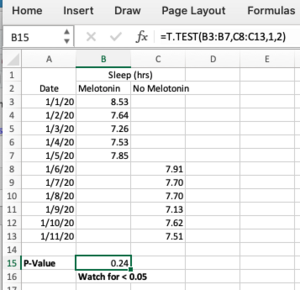
Here’s an example for how to do a t-test in Excel. It uses the example of evaluating the impact of taking melatonin on sleep duration.
Your simple spreadsheet might look like this:
Track your sleep under two columns: one for nights when you took the supplement, and the other for nights you didn’t.
The built-in Excel statistical function T.TEST will calculate the p-value when you give it two ranges[2], one for the “intervention” (the nights we took Melatonin) and the “control” (the nights without).
The formula for doing the t-test is this (see the screenshot for the exact formula in the example):
=T.TEST(array1,array2,tails,type)
Enter a 1 for tails (because we’re only interested in one direction of increasing sleep) and a 2 for type (because in this case our samples are not paired but from independent nights of sleep).
The p-value in this example, 0.24, is above 0.05 and therefore we will assume that any difference in sleep between the nights is due to pure chance.
t-tests in R[edit | edit source]
You can do the same t-test in the statistical programming language R, using the same example:
melatonin <- c(8.53,7.64,7.26,7.53,7.85) # load intervention data no_melatonin <- c(7.91,7.7,7.7,7.13,7.62,7.51) # load control data t.test(melatonin,no_melatonin,alternative='greater',paired=FALSE) # run the t-test
First we load both data series into R and then run the actual t-test. With alternative='greater' we specify a one-sided t-test in which we test whether the values of the intervention data are larger than those of the control. Alternatively we could have chosen alternative='less' or alternative='two.sided'. With paired=FALSE we specify that these are independent, non-paired samples.
Running our test results in the following output:
Welch Two Sample t-test
data: melatonin and no_melatonin
t = 0.69689, df = 5.9576, p-value = 0.2561
alternative hypothesis: true difference in means is greater than 0
95 percent confidence interval:
-0.2992509 Inf
sample estimates:
mean of x mean of y
7.762 7.595
We see that p-value = 0.2561, indicating that the sleep-duration when taking melatonin is not substantially larger compared to the control and that any differences are likely just by chance.
Limitations[edit | edit source]
T-tests remain an easily and widely used statistical tool to investigate whether observed differences between conditions are likely to be due to random chance or not. One of the main limitations of t-tests is that they only work for comparisons between exactly two groups. If you try to do more complex interventions/experiments, the t-test might not work for you.
Technical, statistical aspects[edit | edit source]
The standard t-test also expects that your measurements (or pairs of measurements in the case of paired tests) are independent of each other. Depending on what you are measuring this might not be the case, in particular for time-series data where you take very frequent samples (e.g. two heart rate measurements taken a minute apart will be highly linked to each other).
The t-test also expects that the underlying data follow a normal distribution[3]. While a large number of biological phenomena seem to generate normally distributed data, this might not be true for a specific case. In those cases, the t-test might lead to wrong conclusions and other statistical tests which don't assume normally distributed data (such as the Mann–Whitney–Wilcoxon test) can be more appropriate.